Tour de France: What are the chances of breakaway success?
Ghent University professor develops the winning formula




A Belgian mathematics professor created a formula to calculate the distance at which the peloton has to start its chase in order to catch the breakaway, or not. The formula was published in Belgian newspaper Het Nieuwsblad, together with a calculator. Cyclingnews worked together with Het Nieuwsblad to create and test a calculator. The big question: will the breakaway make it or not?
Hendrik Van Maldeghem is a math professor at the Ghent University. He worked his way through historical data from races and started building a formula. He discovered that once a breakaway group is larger than nine riders its size no longer matters to calculate fatigue. When the group was smaller than ten riders the formula became more challenging as the fatigue becomes a much more important factor. Other parameters in the formula are the speed in both the breakaway group and in the peloton and of course the gap between the breakaway group and the peloton.
This speed isn't easy to pinpoint as one should wonder whether to take the current speed, the average speed over three kilometres or maybe the average speed over the whole race. The leaders might be riding on a false flat road while the peloton descends of a climb, which means the actual speed doesn't seem to provide the most accurate numbers. The professor didn't take into account the profile of the course, the wind or other parameters.
During the two first flat stages of the Tour de France the calculator was tested and it proved to be rather accurate. The formula was also tested in stage 2 when Jasper Stuyven (Trek-Segafredo) his breakaway attempt stranded in the final 500 metres. The formula predicted the breakaway would make it but the climbs in the final kilometres created more fatigue with the breakaway riders. The formula provides a rather accurate distance once the maximum advantage is reached by the breakaway group.
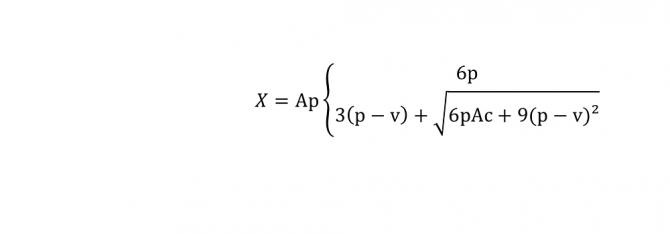
X = distance at which the peloton should start chasing in kilometres
A = time gap between the breakaway group and the peloton in hours
p = speed of the peloton in kilometres an hour
v = speed of the breakaway group in kilometres an hour
c = 10-a
a = amount of riders in the breakaway group
Professor Van Maldeghem told in Het Nieuwsblad: "After checking the individual time trials I take into account that the speed of a breakaway rider drops by 1 km/h per 20 minutes once the peloton starts chasing. That speed loss is reduced proportionally in combination with the amount of riders in the breakaway until it reaches zero, when there are 10 riders in the breakaway group. By expressing the loss of speed per time instead of per distance an equation of accelerated motion which leads to a exact solvable equation without having to approximate."
The latest race content, interviews, features, reviews and expert buying guides, direct to your inbox!
- Tour de France stage 4 finish line quotes
- Tour de France stage 4 highlights - Video
- Tour de France: Sagan defeated but happy in Limoges
- Tour de France: Kittel wins stage 4 in Limoges
- Tour de France: Froome tips Valverde to take yellow on stage 5